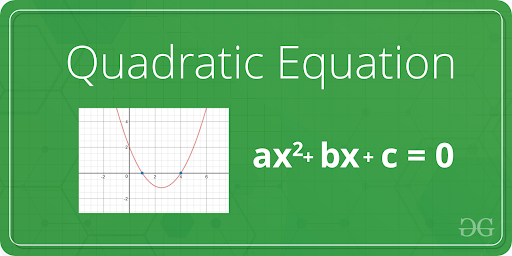A free online application called the discriminant calculator determines the discriminant value for a quadratic equation’s given coefficients. The online discriminant calculator tool can facilitate quicker and easier computations by displaying the number in a matter of seconds.
How Can I Use This Calculator to Discriminate?
Here is the method to use the discriminant calculator:
Step 1
Fill in the designated input fields with the coefficient values, such as “a,” “b,” and “c.”
Step 2
To obtain the result, click the “Solve” button now.
Step 3
The output will be your discriminant value.
Definition of Discriminant
A discriminant expresses the kind of roots of a particular quadratic equation as a function of the coefficients of a polynomial equation. The formulas are capable of differentiating between the following probable answers:
There are two viable options in cases where the discriminant value is positive.
There is only one viable solution when the discriminant value is zero.
Two intricate solutions arise when the discriminant value is negative.
Standard Form
The standard discriminant form for the quadratic equation ax2 + bx + c = 0 is
Discriminant, D = b2 – 4ac
Where
a is the coefficient of x2
b is the coefficient of x
c is a constant term.
What Makes the Discriminant Value in a Quadratic Equation Significant?
A discriminant value can be used to determine the kind of roots in a quadratic equation. The quadratic equation can have real or complex roots. Finding an equation’s solution is one of its uses.
How may the Discriminant Value be Used to Determine the Kind of Roots?
The roots of a quadratic equation can take many forms. The discriminant value is use to identify the kind of roots. These are:
Real and unequal roots exist if D > 0.
The roots are equivalent and real if D = 0.
The roots are complicated, or not real if D is less than 0.
What do Discriminants that are Positive and Negative Mean?
Two distinct real number solutions to the quadratic are indicate by a positive discriminant. When the discriminant is 0, it indicates that the quadratic is made up of several real number solutions. When there is a negative discriminant, it means that none of the solution values is real.
Why Opt for Our Calculator with Discrimination?
Accuracy: The calculator guarantees that all computations are free of errors and produces precise results every time. Easily Use Our Discriminant Calculator has an intuitive UI that makes it simple to use. Enter your quadratic equation, and the program will take care of the rest.
Methodical SolutionsThis calculator not only gives you the discriminant value but also a methodical solution. Because of this characteristic, it’s a great learning aid for anyone attempting to comprehend how the calculation works.
Quickness outcomes right away! You may save time and effort by using our calculator to solve any quadratic problem rapidly.
Important Things to Consider
Because it indicates the number of solutions to any given quadratic equation, the discriminant is significant.
- There are two options if the discriminant is a positive number.
- The answer will be one if the discriminant is zero.
- True solutions won’t exist if the discriminant is a negative value.
The number of roots of a quadratic equation can be determined by counting the solutions to the equation. The points on the quadratic graph where the 𝑥-axis is crossed are the roots of a quadratic equation. These are intercepts on the 𝑥-axis.
How to Calculate the Discriminant
Formula b2 – 4ac can be use to find discriminant values. Substitute the values of a, b, and c after reading them from a quadratic equation of the form a𝑥2 + b𝑥 + c. For example, for 𝑥2 – 3𝑥 + 4, a = 1, b = -3 and c = 4. b2 = 9 and 4ac = 16. The discriminant, b2 – 4ac = – 7.
These crucial factors should be taken into account while computing the discriminant:
B2 is consistently positive. Positive results are obtain when we square a negative number.
The addition must be done if 4ac is negative. An addition occurs when we subtract a negative amount.
How To Find the Discriminant
Find a, which is the coefficient of 𝑥2.
And Find b, which is the coefficient of 𝑥.
And Find c, which is the constant term.
Square the b value to find b2.
Multiply 4 × a × c to find 4ac.
Use these values to calculate b2 – 4ac.
Discriminant Calculator: Main Points
To use the discriminant calculator:
Read the coefficient of 𝑥2 to find ‘a’.
And Read the coefficient of 𝑥 to find ‘b’.
And Read the constant term which is ‘c’.
A Discriminant in Positive
When b2–4ac has a positive discriminant, it indicates that the value is higher than zero. There are exactly two solutions to a quadratic equation with a positive discriminant, indicating that it has two 𝑥-axis intercepts. In other words, the quadratic has two roots.
A positive value of the discriminant means that the graph of the quadratic equation must pass through the 𝑥-axis twice.
If the quadratic has a positive coefficient of 𝑥2 (a > 0), the graph is concave up and the minimum point will be below the 𝑥-axis as shown in the left image below.
If the quadratic has a negative coefficient of 𝑥2 (a < 0), the graph is concave down and the minimum point will be above the 𝑥-axis as shown in the right image below.
Conclusion
A free online application called the discriminant calculator determines the discriminant value for a quadratic equation’s given coefficients.